K-means clustering for faster collaborative filtering
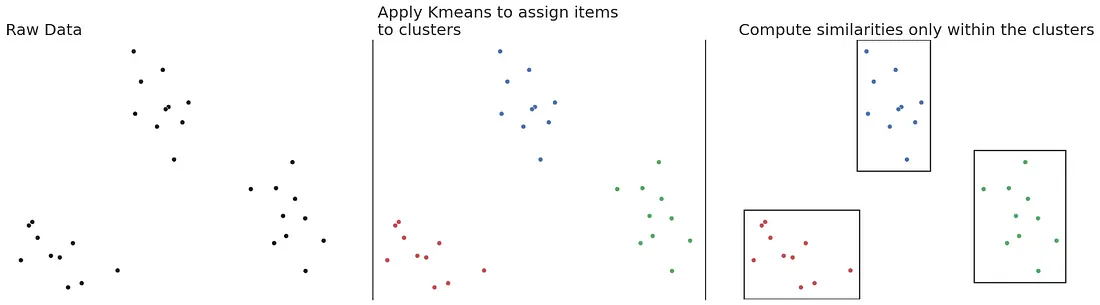
The classical collaborative filtering approach includes computing the cosine distance between all pairs of users or items. In the book Practical Recommeder Systems the author proposes a simple way to reduce this computational burden — apply K-means clustering and only compute the cosine distance intra-cluster. The rest of this article will attempt to benchmark this idea on the MovieLens dataset.
For the default implementation, we will simply use the cosine_similarity function from sklearn. For example, given a matrix M:
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(M, M, dense_output=False)
The patched implementation is as follows:
- compute KMeans on the full dataset
- for each cluster compute the cosine similarity between items in the cluster
def cosine_similarity_kmeans(m, num_clusters=4):
kmeans = KMeans(num_clusters,n_init=3,max_iter=1000)
kmeans.fit(m)
labels = kmeans.labels_
sims = []
for cluster_id in range(num_clusters):
cluster_rows = m[labels==cluster_id]
if cluster_rows.shape[0]< 10:
display(f"WARNING: small cluster with only {cluster_rows.shape[0]} rows")
sim = cosine_similarity(cluster_rows, cluster_rows, dense_output=False)
sims.append(sim)
return sims, kmeans
For a varying number of clusters, I ran the algorithm on the first 40k users from the ML dataset. The times were as follows:
As we can see, with the appropriate number of clusters, we can decrease the processing time from 51 seconds to 17 seconds.
To recap: we can leverage a clustering algorithm to split the dataset into higher-density clusters and only compute similarities between pairs of items in their respective clusters. We used this technique on a subset of the MovieLens dataset and achieved a speedup of 66%.